【改编】（本小题满分8分）
“6”字形图中，FM是大⊙O的直径，BC与大⊙O相切于B，OB与小⊙O相交于点A，AD∥BC，CD∥BH∥FM，DH⊥BH于H，设∠FOB＝α，OB＝4，BC＝6．
（1）求证：AD为小⊙O的切线；
|
（2）在图中找出一个可用α表示的角，并说明你这样表示的理由；（根据所写结果的正确性及所需推理过程的难易程度得分略有差异）
（3）当α＝30º时，求DH的长。（结果保留根号)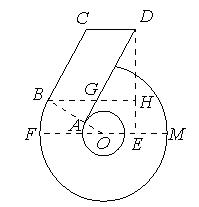
相关知识点
推荐套卷
【改编】（本小题满分8分）
“6”字形图中，FM是大⊙O的直径，BC与大⊙O相切于B，OB与小⊙O相交于点A，AD∥BC，CD∥BH∥FM，DH⊥BH于H，设∠FOB＝α，OB＝4，BC＝6．
（1）求证：AD为小⊙O的切线；
|
（2）在图中找出一个可用α表示的角，并说明你这样表示的理由；（根据所写结果的正确性及所需推理过程的难易程度得分略有差异）
（3）当α＝30º时，求DH的长。（结果保留根号)
粤公网安备 44130202000953号