(本小题满分13分)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
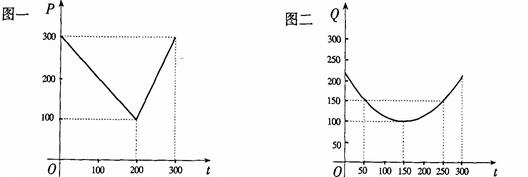 |
(Ⅰ) 写出图一表示的市场售价与时间的函数关系式P =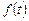 ;
;
写出图二表示的种植成本与时间的函数关系式Q =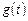 ;
;
(Ⅱ) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/ kg,时间单位:天)
kg,时间单位:天)
相关知识点
推荐套卷
 ,点
,点 依次满足
依次满足 。
。 的轨迹;
的轨迹; 作直线
作直线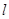 交以
交以 为焦点的椭圆于
为焦点的椭圆于 两点,线段
两点,线段 的中点到
的中点到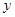 轴的距离为
轴的距离为 ,且直线
,且直线 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点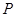 及以
及以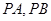 都相切,如存在,求出
都相切,如存在,求出
 .现已知相距18
.现已知相距18 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设 (
( 的函数; (2)若
的函数; (2)若 ,且
,且 时,
时, 的值.
的值.
 中,角
中,角 所对的边分别为
所对的边分别为 。已知
。已知 ,
, .
. ,求
,求 的值.
的值.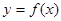 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意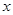 ,存在实数
,存在实数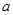 使得
使得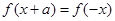 成立,则称此函数具有“
成立,则称此函数具有“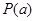 性质”。
性质”。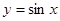 是否具有“
是否具有“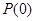 性质”,且当
性质”,且当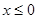 时
时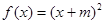 ,求
,求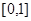 上有最大值;
上有最大值;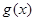 具有“
具有“ 性质”,且当
性质”,且当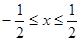 时,
时,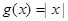 .若
.若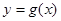 与
与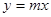 交点个数为2013,求
交点个数为2013,求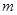 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号