(本小题满分12分) 已知函数f(x)=ax2+bx+c(a>0,b∈R, c∈R).
(Ⅰ)若函数f(x)的最小值是f(-1)=0,且c=1,
,
求F(2)+F(-2)的值
(Ⅱ)若a=1,c=0,且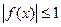
在区间(0,1]上恒成立，试求b的取值范围。
中，
，
，求
．
的首项
，前
项和为
，且
．
是等比数列；
，求函数
在点
处的导数
，并比较
与
的大小．
的通项公式为
．
是否是数列
，求
．
的不等式：
．
，且
，若
构成公差为
的等差数列．
和
表示
；
是满足
的整数，则当
时，数列相关知识点
推荐套卷
(本小题满分12分) 已知函数f(x)=ax2+bx+c(a>0,b∈R, c∈R).
(Ⅰ)若函数f(x)的最小值是f(-1)=0,且c=1,,
求F(2)+F(-2)的值
(Ⅱ)若a=1,c=0,且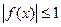在区间(0,1]上恒成立，试求b的取值范围。
粤公网安备 44130202000953号