（本小题满分10分）
某地区为下岗女职工免费提供财会和家政培训，以提高下岗女职工的再就业能力，每名下岗人员可以参加一项培训、参加两项培训或不参加培训，已知参加过财会培训的有50%，参加过家政培训的有80%，假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响
（1）任选1名下岗女职工，求该人参加过培训的概率
（2）任选3名下岗女职工，记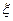
为3人中参加过培训的人数，求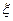的分布列和期望
相关试题
中，
，
，各项为正数的等比数列
中，
，
．
，求数列
的前
项和
．
，若
满足
，
，
，求
及
的长．
的解集为
，
．
，
的值；
，
，若
是
的充分条件，求实数
的取值范围．
中，
分别
的中点，
，
．
；
与
所成角的余弦值；
中，平面
平面
，
平面
， 
．且
，
．
平面
；
的余弦值。推荐套卷
（本小题满分10分）
某地区为下岗女职工免费提供财会和家政培训，以提高下岗女职工的再就业能力，每名下岗人员可以参加一项培训、参加两项培训或不参加培训，已知参加过财会培训的有50%，参加过家政培训的有80%，假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响
（1）任选1名下岗女职工，求该人参加过培训的概率
（2）任选3名下岗女职工，记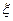为3人中参加过培训的人数，求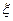的分布列和期望
粤公网安备 44130202000953号