小学三年级的英语老师要求学生从星期一到星期四每天学习英语单词3个;每周星期五对一周内所学单词随机抽取4个进行检测(一星期所学的单词每个被抽到的可能性相同);
(1)求英语老师随机抽到的4个单词中,至少含有3个离周五最近两天学习过的概率;
(2)某学生在周五检测中,对其最近两天所学过的单词每个能默写对的概率为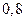 ,对周一和周二的单词每个能默写对的概率为
,对周一和周二的单词每个能默写对的概率为 ;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数
;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数 的分布列和期望.
的分布列和期望.
推荐套卷
小学三年级的英语老师要求学生从星期一到星期四每天学习英语单词3个;每周星期五对一周内所学单词随机抽取4个进行检测(一星期所学的单词每个被抽到的可能性相同);
(1)求英语老师随机抽到的4个单词中,至少含有3个离周五最近两天学习过的概率;
(2)某学生在周五检测中,对其最近两天所学过的单词每个能默写对的概率为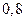 ,对周一和周二的单词每个能默写对的概率为
,对周一和周二的单词每个能默写对的概率为 ;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数
;现已知老师从周一到周四每天的单词中各抽取了一个单词进行检测,求该学生能默写对的单词数 的分布列和期望.
的分布列和期望.