袋中有大小相同的4个红球，6个白球，每次从中摸取一球，每个球被取到的可
能性相同，现不放回地取3个球.
（1）求第三个取出红球的概率；
（2）求至少取到两个红球的概率；
（3）（理）用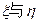
分别表示取得的红球数与白球数，计算
、
、
、
.
相关试题
对应的复数为
，过点
，设
,试求复数
对应的点集是什么图形？
是实数，且
；
的实部和虚部都是整数．
，且
为纯虚数，求
的最大值及当
取最大值时的
．
的两个顶点
对应的复数分别为
、
．求另外两个顶点
对应的复数．
取何值时，复数
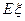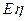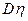推荐套卷
袋中有大小相同的4个红球，6个白球，每次从中摸取一球，每个球被取到的可
能性相同，现不放回地取3个球.
（1）求第三个取出红球的概率；
（2）求至少取到两个红球的概率；
（3）（理）用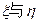分别表示取得的红球数与白球数，计算、、、.
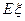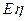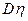粤公网安备 44130202000953号