已知函数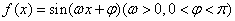 的周期为
的周期为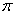 ,图像的一个对称中心为
,图像的一个对称中心为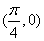 ,
,
将函数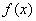 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移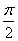 个单位
个单位
长度后得到函数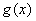 的图像.
的图像.
(1)求函数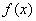 与
与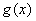 的解析式;
的解析式;
(2)是否存在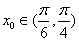 ,使得
,使得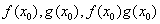 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定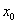 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
(3)求实数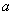 与正整数
与正整数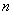 ,使得
,使得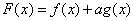 在
在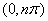 内恰有2013个零点.
内恰有2013个零点.
相关知识点
推荐套卷
已知函数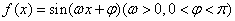 的周期为
的周期为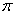 ,图像的一个对称中心为
,图像的一个对称中心为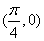 ,
,
将函数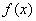 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移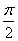 个单位
个单位
长度后得到函数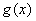 的图像.
的图像.
(1)求函数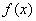 与
与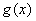 的解析式;
的解析式;
(2)是否存在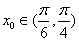 ,使得
,使得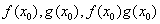 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定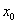 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
(3)求实数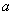 与正整数
与正整数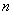 ,使得
,使得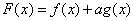 在
在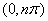 内恰有2013个零点.
内恰有2013个零点.