(本题16分）如图
，正
比例函数和反比例函数的图象都经过点 A ( 3 , 3) ，把直线 OA 向下平移后，与反比例函数的图象交于点B(6,m)，与x轴、y轴分别交于C、D两点。
(1）求 m的值；
( 2 ）求过 A、B、D 三点的抛物线的解析式；
( 3 ）若点E是抛物线上的一个动点，是否存在点 E
，使四边形 OECD 的面积S1，是四边形OACD 面积S的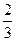
?若存在，求点 E 的坐标；若不存在，请说明理由．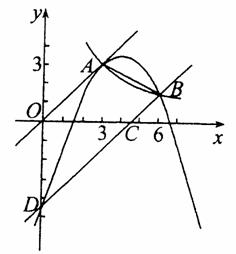
；
，且
异号，
是绝对值最小的负整数，
，求3A·B-
A·C的值.
，其中
.相关知识点
推荐套卷
(本题16分）如图，正比例函数和反比例函数的图象都经过点 A ( 3 , 3) ，把直线 OA 向下平移后，与反比例函数的图象交于点B(6,m)，与x轴、y轴分别交于C、D两点。
(1）求 m的值；
( 2 ）求过 A、B、D 三点的抛物线的解析式；
( 3 ）若点E是抛物线上的一个动点，是否存在点 E，使四边形 OECD 的面积S1，是四边形OACD 面积S的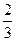?若存在，求点 E 的坐标；若不存在，请说明理由．
粤公网安备 44130202000953号