（本小题 9 分）某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市 20000 名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如下图表：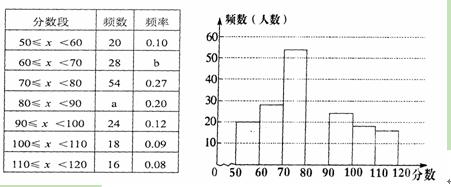
（1）表中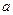
和
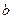所表示的数分别为：=_______________，=_______________；
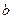（2）请在图中补全额数分布直方图；
（3）如果把成绩在70分以上（含70分）定为合格，那么该市20000名九年级考生数学成绩为合格的学生约有多少名？
相关试题
近年来，国家实施“村村通”工程和农村医疗卫生改革，某县计划在张村、李村之间建一座定点医疗站P，张、李两村座落在两相交公路内（如图所示）．医疗站必须满足下列条件：①使其到两公路距离相等；②到张、李两村的距离也相等．请你通过作图确定P点的位置．
某车间有16名工人，每人每天可加工甲种零件5个或乙种零件4个．在这16名工人中，一部分人加工甲种零件，其余的加工乙种零件．已知每加工一个甲种零件可获利16元，每加工一个乙种零件可获利24元．若此车间一共获利1 440元，求这一天有几名工人加工甲种零件．
﹥
＞
．
．
，
，
，请说明
的值与
的取值无关．相关知识点
推荐套卷
粤公网安备 44130202000953号