(本小题满分12分)某区组织群众性登山健身活动,招募了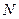 名师生志愿者,将所有志愿者现按年龄情况分为
名师生志愿者,将所有志愿者现按年龄情况分为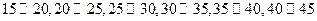 等六个层次,其频率分布直方图如图所示: 已知
等六个层次,其频率分布直方图如图所示: 已知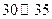 之间的志愿者共
之间的志愿者共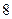 人.
人.
(Ⅰ)求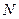 和
和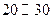 之间的志愿者人数
之间的志愿者人数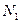 ;
;
(Ⅱ)已知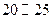 和
和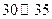 之间各有
之间各有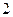 名英语教师,现从这两个层次各选取
名英语教师,现从这两个层次各选取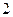 人担任接待工作,设两组的选择互不影响,求两组选出的人选中都至少有1名英语教师的概率是多少?
人担任接待工作,设两组的选择互不影响,求两组选出的人选中都至少有1名英语教师的概率是多少?
(Ⅲ)组织者从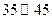 之间的志愿者(其中共有
之间的志愿者(其中共有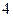 名女教师,其余全为男教师)中随机选取
名女教师,其余全为男教师)中随机选取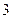 名担任后勤保障工作,其中女教师的数量为
名担任后勤保障工作,其中女教师的数量为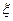 ,求
,求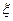 的概率和分布列.
的概率和分布列.
推荐套卷
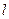 的倾斜角的正弦值为
的倾斜角的正弦值为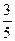 ,且它与坐标轴围成的三角形的面积为
,且它与坐标轴围成的三角形的面积为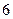 ,求直线
,求直线 ,
,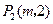 的直线
的直线 的方程(其中
的方程(其中 ).
). ,并且和两条直线
,并且和两条直线 与
与 都相交,且两交点的中点是
都相交,且两交点的中点是 ,求这条直线的方程.
,求这条直线的方程. ,
, .
. 为何值时,
为何值时, :(1)相交;(2)平行.
:(1)相交;(2)平行. ,
,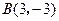 ,
, ,求
,求 边所在直线的方程,以及该边上中线所在直线的方程.
边所在直线的方程,以及该边上中线所在直线的方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号