(本题20分) (湖南湘西,25,20分)如图.抛物线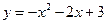
与x轴相交于点A和点B,与y轴交于点C.
(1)求点A、点B和点C的坐标.
(2)求直线AC的解析式.
(3)设点M是第二象限内抛物线上的一点,且
=6,求点M的坐标.
(4)若点P在线段BA上以每秒1个单位长度的速度从A运动(不与B,A重合),同时,点Q在射线AC上以每秒2个单位长度的速度从A
向C运动.设运动的时间为t秒,请求出△APQ的面积S与t的函数关系式,并求出当t为何值时, △APQ的面积最大,最大面积是多少?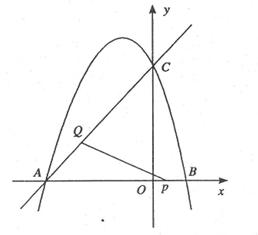
相关试题
把下列各式分解因式
（1）m2（m﹣n）2﹣4（n﹣m）2
（2）x2﹣4﹣4xy+4y2
（3）（3x2﹣4x+3）2﹣（2x2﹣x﹣7）2
（4）
（5）x（x+1）3+x（x+1）2+x（x+1）+x+1．
把下列各式分解因式：
①3（a+b）2﹣27c2
②16（x+y）2﹣25（x﹣y）2
③a2（a﹣b）+b2（b﹣a）
④（5m2+3n2）2﹣（3m2+5n2）2
分解因式：
（1）a2x2y﹣axy2（2）x（x﹣y）﹣y（y﹣x）
（3）9（a﹣b）2﹣16（a+b）2（4）25（x﹣y）2+10（y﹣x）+1
（5）﹣3x3+12x2y﹣12xy2（6）m（x﹣y）2﹣x+y．
相关知识点
推荐套卷
粤公网安备 44130202000953号