已知:如图9,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=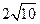
 .
.
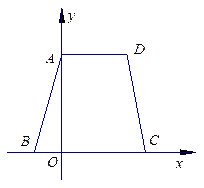
(1)求点B的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,
|
使得 ?若存在,请求出该点坐标,
?若存在,请求出该点坐标,
相关知识点
推荐套卷
已知:如图9,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=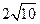
 .
.

(1)求点B的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,
|
使得 ?若存在,请求出该点坐标,
?若存在,请求出该点坐标,