如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.
(1)求EG的长;
(2)求证:CF=AB+AF.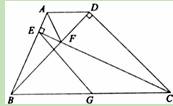
相关知识点
推荐套卷
如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.
(1)求EG的长;
(2)求证:CF=AB+AF.