如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒得速度从A点出发,沿AC向C移动,同时,动点Q以1米/秒得速度从C点出发,沿CB向B移动。当其中有一点到达终点时,他们都停止移动,设移动的时间为t秒。
(1)①当t=2.5秒时,求△CPQ的面积;
②求△CPQ的面积S(平方米)关于时间t(秒)的函数关系式;
(2)在P、Q移动的过程中,当△CPQ为等腰三角形时,写出t的值;
(3)以P为圆心,PA为半径的圆与以Q为圆心,QC为半径的圆相切时,求出t的值。
相关知识点
推荐套卷
 ,AD=7,AH=
,AD=7,AH= .现有两个动点E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运动到点C时,E、F两点同时停止运动. 设运转时间为t秒.
.现有两个动点E、F同时从点A出发,分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中,以EF为边作等边△EFG,使△EFG与△ABC在射线AC的同侧,当点E运动到点C时,E、F两点同时停止运动. 设运转时间为t秒.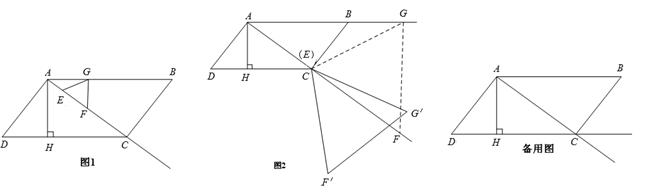
 . 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.
. 在旋转过程中,点E与点C重合,F的对应点为F′,G的对应点为G′. 设直线F′G′与射线DC、射线AC分别相交于M、N两点.试问:是否存在点M、N,使得△CMN是以∠MCN为底角的等腰三角形?若存在,请求出线段CM的长度;若不存在,请说明理由.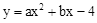 与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.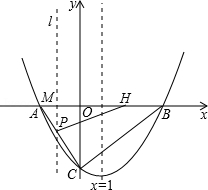
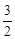 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点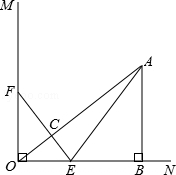
 S四边形ABOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形ABOF?若存在,请求出此时t的值;若不存在,请说明理由.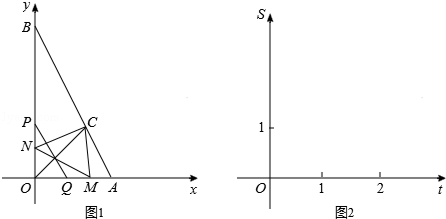
 粤公网安备 44130202000953号
粤公网安备 44130202000953号