（本题满分18分
）第一题满分5分，第二题满分5分，第三题满分8分．
如图，有一公共边但不共面的两个三角形ABC和A1BC被一平面DEE1D1所截，若平面DEE1D1分别交AB,AC,A1B,A1C于点D,E,D1,E1。
（1）讨论这三
条交线ED,CB, E1 D1的关系。
（2）当BC//平面DEE1D1时,求
的值;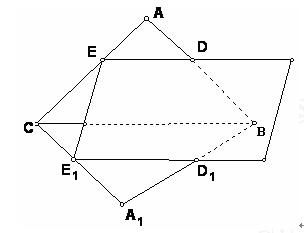
（3）当BC不平行平面DEE1D1时, 的值变化吗？为什么？
相关试题
的切线
,交椭圆G于A，B两点.
表示为m的函数，并求
中，
⊥平面
,
，
与底面
， 
.
∥平面
，求
的值；
等于何值时，二面角
的大小为45°？
中，角
所对的
边为
，已知
。
的值；
，且
，求
}中，
，并且对任意
都有
成立，令
．
}的通项公式；（Ⅱ）求数列{
}的前n项和
，不等式
恒成立，求实数
的取值范围；
，满足不等式
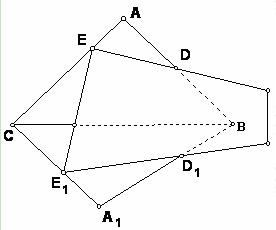
，求实数推荐套卷
（本题满分18分）第一题满分5分，第二题满分5分，第三题满分8分．
如图，有一公共边但不共面的两个三角形ABC和A1BC被一平面DEE1D1所截，若平面DEE1D1分别交AB,AC,A1B,A1C于点D,E,D1,E1。
（1）讨论这三条交线ED,CB, E1 D1的关系。
（2）当BC//平面DEE1D1时,求的值;
（3）当BC不平行平面DEE1D1时, 的值变化吗？为什么？
粤公网安备 44130202000953号