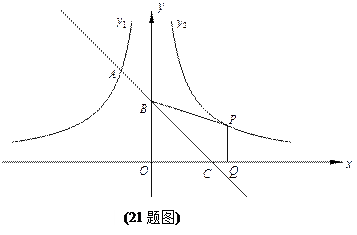
如图，一次函数的图象与反比例函数y1=" –" ( x<0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0).当x<–1时，一次函数值大于反比例函数的值，当x>–1时，一次函数值小于反比例函数值.
(1) 求一次函数的解析式；
(2) 设函数y2= (x>0)的图象与y1=" –" (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P（P点的横坐标大于2)，过P作PQ⊥x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标.
 |
如图，一次函数的图象与反比例函数y1=" –" ( x<0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0).当x<–1时，一次函数值大于反比例函数的值，当x>–1时，一次函数值小于反比例函数值.
(1) 求一次函数的解析式；
(2) 设函数y2= (x>0)的图象与y1=" –" (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P（P点的横坐标大于2)，过P作PQ⊥x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标.
|
，则
的值为多少？
，求分式
的值。
，其中a=
，b=－3
，其中x=2．
粤公网安备 44130202000953号