(本小题满分10分)
在复习《反比例函数》一课时,同桌的小明和小芳有一个间题观点不一致,小明认为如果两次分别从l到6六个整数中任取一个数,第一个数作为点 的横坐标,第二个数作为点
的横坐标,第二个数作为点 的纵坐标,则点
的纵坐标,则点 在反比例函数
在反比例函数 的的图象上的概率一定大于在反比例函数
的的图象上的概率一定大于在反比例函数 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点 的情形;
的情形;
(2)分别求出点 在两个反比例函数的图象上的概率,并说明谁的观点正确。
在两个反比例函数的图象上的概率,并说明谁的观点正确。
相关知识点
推荐套卷
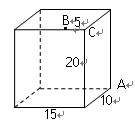
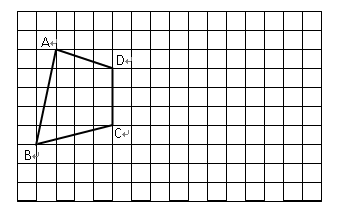
 绕点C沿顺时针旋转90°得到四边形A1B1CD1;
绕点C沿顺时针旋转90°得到四边形A1B1CD1;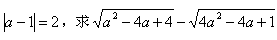 的值
的值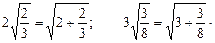
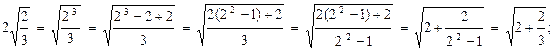
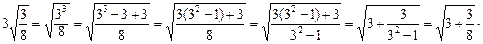
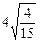 的结果,并写出验证过程;
的结果,并写出验证过程;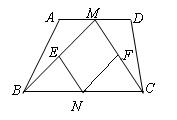
 粤公网安备 44130202000953号
粤公网安备 44130202000953号