在直角坐标系xOy中,椭圆C1: 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: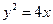 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
.
(Ⅰ)求C1的方程;
(Ⅱ)平面上的点N满足 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
·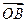 =0,求直线l的方程.
=0,求直线l的方程.
推荐套卷
在直角坐标系xOy中,椭圆C1: 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: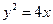 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
.
(Ⅰ)求C1的方程;
(Ⅱ)平面上的点N满足 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
·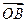 =0,求直线l的方程.
=0,求直线l的方程.