(本小题满分8分)某种产品的质量以其质量指标值衡量,质量指标值大于或等于98且小于106的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表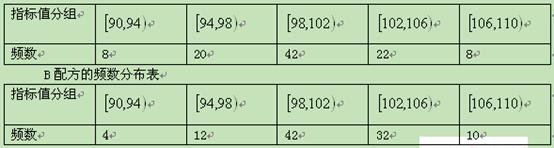
(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)由以上统计数据填写2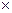 2列联表,问是否有99
2列联表,问是否有99 的把握认为“A配方与B配方的质量有差异”。
的把握认为“A配方与B配方的质量有差异”。
推荐套卷
(本小题满分8分)某种产品的质量以其质量指标值衡量,质量指标值大于或等于98且小于106的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)由以上统计数据填写2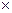 2列联表,问是否有99
2列联表,问是否有99 的把握认为“A配方与B配方的质量有差异”。
的把握认为“A配方与B配方的质量有差异”。