(本小题满分12分)根据市气象站 对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线
对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(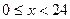 ,单位为小时,
,单位为小时,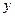 表示气温,单位为摄氏度,
表示气温,单位为摄氏度, ,
, ,现已知这天气温为4至12摄氏度,并得知在凌晨1时整
,现已知这天气温为4至12摄氏度,并得知在凌晨1时整 气温最低,下午13时整气温最高。
气温最低,下午13时整气温最高。
(1)求这条曲线的函数表达式;
(2)求这一天19时整的气温。
推荐套卷
(本小题满分12分)根据市气象站 对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线
对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(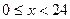 ,单位为小时,
,单位为小时,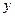 表示气温,单位为摄氏度,
表示气温,单位为摄氏度, ,
, ,现已知这天气温为4至12摄氏度,并得知在凌晨1时整
,现已知这天气温为4至12摄氏度,并得知在凌晨1时整 气温最低,下午13时整气温最高。
气温最低,下午13时整气温最高。
(1)求这条曲线的函数表达式;
(2)求这一天19时整的气温。