(本小题满分8分)在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连结EG、CG,如图(1),易证 EG=CG且EG⊥CG.
(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和
位置关系?请直接写出你的猜想.
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系
和位置关系?请写出你的猜想,并加以证明.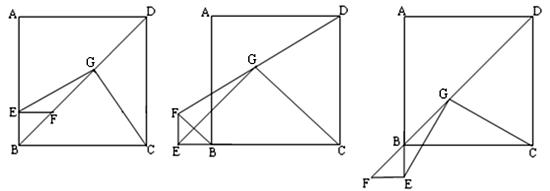
相关知识点
推荐套卷
(本小题满分8分)在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连结EG、CG,如图(1),易证 EG=CG且EG⊥CG.
(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和
位置关系?请直接写出你的猜想.
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系
和位置关系?请写出你的猜想,并加以证明.