．(本小题满分14分)
已知一几何体的三视图如图(甲)示，(三视图中已经给出各投影面顶点的标记)
(1)在已给出的一个面上(图乙)，
画出该几何体的直观图
(2)设点F、H、G分别为AC、AD、
DE的中点，求证：FG//平
面ABE；
(3)求该几何体的体积．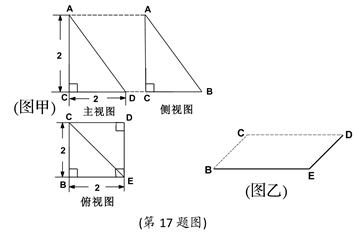
相关试题
，长轴长为6。 
的图象经过点
，且在
处的切线方程是
。（1）求
的解析式；（2）求
中，
，
，
，
，点D是
的中点. 
；
平面
； 
与直线
所成角的余弦值.
；
.推荐套卷
．(本小题满分14分)
已知一几何体的三视图如图(甲)示，(三视图中已经给出各投影面顶点的标记)
(1)在已给出的一个面上(图乙)，
画出该几何体的直观图
(2)设点F、H、G分别为AC、AD、
DE的中点，求证：FG//平面ABE；
(3)求该几何体的体积．
粤公网安备 44130202000953号