已知函数 =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x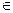 (-∞,-3)
(-∞,-3)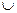 (2,+∞)时,
(2,+∞)时,  <0,当x
<0,当x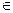 (-3,2)时
(-3,2)时 >0 .
>0 .
(1)求 在[0,1]内的值域.
在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.
相关知识点
推荐套卷
已知函数 =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x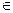 (-∞,-3)
(-∞,-3)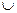 (2,+∞)时,
(2,+∞)时,  <0,当x
<0,当x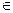 (-3,2)时
(-3,2)时 >0 .
>0 .
(1)求 在[0,1]内的值域.
在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.