（本小题满分12分）
已知椭圆C：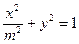
（常数
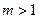），P是曲线C上的动点，M是曲线C的右
顶点，定点A的坐标为(2,0).
（1）若M与A重合，求曲线C的焦点坐标.
（2）若
,求|PA|的最大值与最小值.
（3）若|PA|最小值为|MA|，求实数
的取值范围.
相关试题
，
的值域．
的定义域为[0，1]，求函数
的定义域．（本小题满分12分）已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半，求：
(1) 动点M的轨迹方程；
(2) 若N为线段AM的中点，试求点N的轨迹．
与圆
(其中
) 相外切，且直线
与圆
相切，求
的值.
,直线L: 
取什么实数，L与圆恒交于两点；推荐套卷
（本小题满分12分）
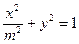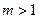已知椭圆C：（常数），P是曲线C上的动点，M是曲线C的右
顶点，定点A的坐标为(2,0).
（1）若M与A重合，求曲线C的焦点坐标.
（2）若,求|PA|的最大值与最小值.
（3）若|PA|最小值为|MA|，求实数的取值范围.
（本小题满分12分）已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半，求：
(1) 动点M的轨迹方程；
(2) 若N为线段AM的中点，试求点N的轨迹．
粤公网安备 44130202000953号