选修4—1：几何证明选讲。如图，PA切圆O于点A，割线PBC经过圆心O，
OB=PB=1，OA绕点O逆时针旋转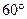
到OD．
（1）求线段PD的长;
（2）在如图所示的图形中是否有长度为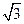
的线段?若有,指出该线段;若没有,说明理由．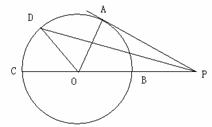
|
或
}，B＝{
或
}，若
，求实数
的取值范围．
，
，求
的值
，对任意
，恒有
．
，
，
的值；
在
上的最值．
的定义域;
的值．
在定义域
上是减函数且为奇函数，若
求实数
的取值范围．推荐套卷
选修4—1：几何证明选讲。如图，PA切圆O于点A，割线PBC经过圆心O，
OB=PB=1，OA绕点O逆时针旋转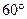到OD．
（1）求线段PD的长;
（2）在如图所示的图形中是否有长度为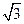的线段?若有,指出该线段;若没有,说明理由．
粤公网安备 44130202000953号