．如图，在平面直角坐标系中，已知点A（0,2），点P是x轴上一动点，以线段AP为一边，在其一侧作等边三角线APQ。当点P运动到原点O处时，记Q得位置为B。
（1）求点B的坐标；
（2）求证：当点P在x轴上运动（P不与Q重合）时，∠ABQ为定值；
（3）是否存在点P，使得以A、O、Q、B为顶点的四边形是梯形？若存在，请求出P点的坐标；若不存在，请说明理由。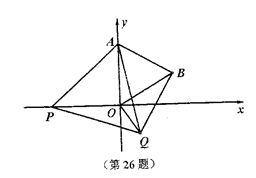
相关试题
中，点
是
边上一动点，过点
∥
，设
的平分线于点
，交
。
；
为怎样的四边形，并证明你的结论；
的一条对角线
平移
的位置，
是等腰三角形吗？为什么？
的对角线
的垂直平分线与边
，
分别交于点
，
，四边形
是否是菱形。
沿
，
同时折叠，
、
两点恰好都落在
边的
点处，若
，
，
，则长方形
为矩形
的对角线的交点，
∥
,
∥
。
的形状，并说明理由；
，
，求四边形相关知识点
推荐套卷
．如图，在平面直角坐标系中，已知点A（0,2），点P是x轴上一动点，以线段AP为一边，在其一侧作等边三角线APQ。当点P运动到原点O处时，记Q得位置为B。
（1）求点B的坐标；
（2）求证：当点P在x轴上运动（P不与Q重合）时，∠ABQ为定值；
（3）是否存在点P，使得以A、O、Q、B为顶点的四边形是梯形？若存在，请求出P点的坐标；若不存在，请说明理由。
粤公网安备 44130202000953号