如图,△ABC的边BC在直线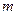 上,AC⊥BC,且AC=BC,△DEF的边FE也在直线
上,AC⊥BC,且AC=BC,△DEF的边FE也在直线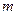 上,边DF与边AC重合,且DF=EF.
上,边DF与边AC重合,且DF=EF.
(1)在图(1)中,请你通过观察、思 考,猜想并写出AB与AE所满足的数量关系和位置关系;(不要求证明)
考,猜想并写出AB与AE所满足的数量关系和位置关系;(不要求证明)
(2)将△DEF沿直线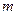 向左平移到图(2)的位置时,DE交AC于点G,连结AE,BG.猜想△BCG与△ACE能否通过旋转重合?请证明你的猜想.
向左平移到图(2)的位置时,DE交AC于点G,连结AE,BG.猜想△BCG与△ACE能否通过旋转重合?请证明你的猜想.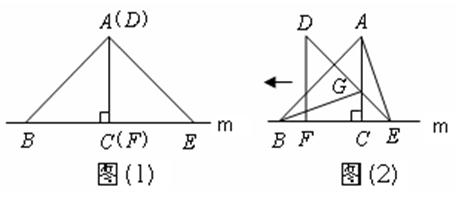
相关知识点
推荐套卷
如图,△ABC的边BC在直线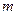 上,AC⊥BC,且AC=BC,△DEF的边FE也在直线
上,AC⊥BC,且AC=BC,△DEF的边FE也在直线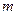 上,边DF与边AC重合,且DF=EF.
上,边DF与边AC重合,且DF=EF.
(1)在图(1)中,请你通过观察、思 考,猜想并写出AB与AE所满足的数量关系和位置关系;(不要求证明)
考,猜想并写出AB与AE所满足的数量关系和位置关系;(不要求证明)
(2)将△DEF沿直线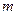 向左平移到图(2)的位置时,DE交AC于点G,连结AE,BG.猜想△BCG与△ACE能否通过旋转重合?请证明你的猜想.
向左平移到图(2)的位置时,DE交AC于点G,连结AE,BG.猜想△BCG与△ACE能否通过旋转重合?请证明你的猜想.