已知
为坐标原点,
为椭圆
在
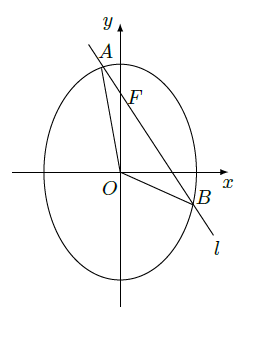
轴正半轴上的焦点,过
且斜率为
的直线
与
交与
两点,点
满足
.
(1)证明:点
在
上;
(2)设点
关于点
的对称点为
,证明:
四点在同一圆上.
推荐套卷
已知
为坐标原点,
为椭圆
在
轴正半轴上的焦点,过
且斜率为
的直线
与
交与
两点,点
满足
.

(1)证明:点
在
上;
(2)设点
关于点
的对称点为
,证明:
四点在同一圆上.