水库的蓄水量随时间而变化,现用t表示时间(单位:月),以年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为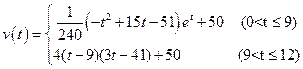 。
。
(1)若该水库的蓄水量小于50的时期称为枯水期,以i-1<t≤i表示第i月份(i=1,2,…12),问一年内那几个月份是枯水期?
(2)求一年内该水库的最大蓄水量(取e3=20计算)。
相关知识点
推荐套卷
水库的蓄水量随时间而变化,现用t表示时间(单位:月),以年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为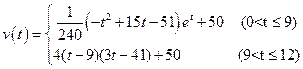 。
。
(1)若该水库的蓄水量小于50的时期称为枯水期,以i-1<t≤i表示第i月份(i=1,2,…12),问一年内那几个月份是枯水期?
(2)求一年内该水库的最大蓄水量(取e3=20计算)。