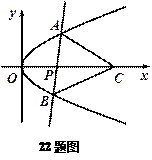设直线l与抛物线y2=2px（p>0）交于A、B两点，已知当直线l经过抛物线的焦点且与x轴垂直时，△OAB的面积为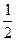
（O为坐标原点）．
（Ⅰ）求抛物线的方程；
（Ⅱ）当直线l经过点P（a，0）（a>0）且与x
轴不垂直时，
若在x轴上存在
点C，使得△ABC为等边三角形，求a
的取值范围．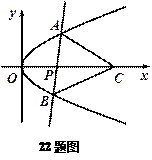
相关试题
，求
的值； 
，求
的值.
.
与圆
相切，且在
轴，
轴上的截距相等，求直线
中.
平面
；
与平面
所成的角.
.
为数列
的前
项和，对任意的
，都有
为常数，且
.
，数列
满足
，
，求数列
的通项公式；
的前
.推荐套卷
设直线l与抛物线y2=2px（p>0）交于A、B两点，已知当直线l经过抛物线的焦点且与x轴垂直时，△OAB的面积为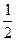（O为坐标原点）．
（Ⅰ）求抛物线的方程；
（Ⅱ）当直线l经过点P（a，0）（a>0）且与x轴不垂直时，
若在x轴上存在点C，使得△ABC为等边三角形，求a
的取值范围．
粤公网安备 44130202000953号