.选修4—4：坐标系与参数方程
以平面直角坐标系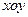
的原点
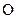为极点，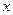
轴的正半轴为极轴建立极坐标系，直线
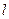的极坐标方程为
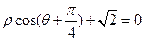，曲线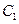
的参数方程为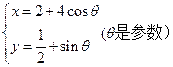
（1）若把曲线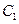上的横坐标缩短为原来的
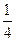，纵坐标不变，得到曲线
，
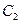求曲线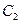在直角坐标系下的方程
（2）在第（1）问的条件下，判断曲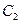线与直线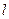的位置关系，并说明理由；
满足
，若
，
且
满足：
，
，
为
。
,求函数的定义域，并讨论它的奇偶性、单调性。
，
，若
,求
的取值范围。
中, 
求
的值。
在（0，1）内是增函数.
的取值范围;
，求证：
.相关知识点
推荐套卷
.选修4—4：坐标系与参数方程
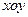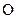以平面直角坐标系的原点为极点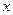，轴的正半轴为极轴建立极坐标系，直线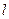的极坐标方程为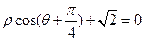，曲线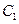的参数方程为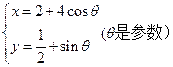
（1）若把曲线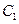上的横坐标缩短为原来的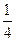，纵坐标不变，得到曲线，
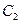求曲线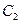在直角坐标系下的方程
（2）在第（1）问的条件下，判断曲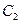线与直线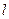的位置关系，并说明理由；
粤公网安备 44130202000953号