(本小题满分12分)
某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本。对高一年级的100名学生的成绩进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图)。
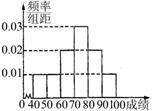
(Ⅰ)若规定60分以上(包括60分)为合格,计算高一年级这次知识
赛的合格率;
(Ⅱ)若高二年级这次知识竞赛的合格率为60%,由以上统计数据填写下 面2×2列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”。
参考数据与公式:
由列联表中数据计算
临界值表
P(K≥k0)
|
0.10
|
0.05
|
0.010
|
k0
|
2.706
|
3.841
|
6.635
|