在△ABC中，BC=6，AC=4，∠C=45o，在BC上有一动点P，过P作PD∥BA与AC相交于点D，连结AP，设BP=x，△APD的面积为y.
（1）求y与x之间的函数关系式，并指出自变量x的取值范围；
（2）是否存在点P，使△APD的面积最大？若存在，求出BP的长，并求出
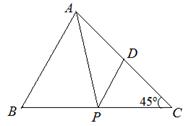△APD面积的最大值.
.
，求
的值．
在同一直线上，
,
，
．
．相关知识点
推荐套卷
在△ABC中，BC=6，AC=4，∠C=45o，在BC上有一动点P，过P作PD∥BA与AC相交于点D，连结AP，设BP=x，△APD的面积为y.
（1）求y与x之间的函数关系式，并指出自变量x的取值范围；
（2）是否存在点P，使△APD的面积最大？若存在，求出BP的长，并求出
△APD面积的最大值.
粤公网安备 44130202000953号