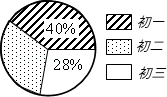
海口市进行课程改革已经七年了，为了了解学生对数学实验教材的喜欢程度，现对某中学初中学生进行了一次问卷调查，具体情况如下：

喜欢程序	非常喜欢	喜欢	不喜欢
人数	600人	500	100人

①已知该校初一共有480人，求该校初中学生总数．
②求该校初二学生人数及其扇形的圆心角度数．
③请补全统计表．
④请计算不喜欢此教材的学生的频率，并对不喜欢此教材的同学提出一条建议，希望能通过你的建议让他喜欢上此教材．