
某学校餐厅新推出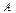 、
、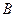 、
、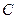 、
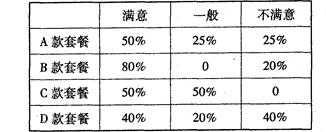
、 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:
(1) 若同学甲选择的是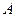 款套餐,求甲的调查问卷被选中的概率;
款套餐,求甲的调查问卷被选中的概率;
(2) 若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这2人中至少有一人选择的是 款套餐的概率。
款套餐的概率。
推荐套卷


某学校餐厅新推出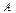 、
、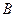 、
、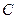 、
、 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:
(1) 若同学甲选择的是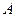 款套餐,求甲的调查问卷被选中的概率;
款套餐,求甲的调查问卷被选中的概率;
(2) 若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这2人中至少有一人选择的是 款套餐的概率。
款套餐的概率。