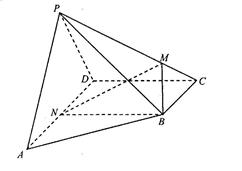
.
如图，四棱锥P-ABCD的侧面PAD垂直于底面ABCD，∠ADC=∠BCD=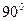
,PA=PD=AD=2BC=2，CD
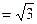,M在棱PC上，N
是AD的中点，二面角M-BN-C为
.
（1）求
的值；
（2）求直线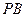
与平面BMN所成角的大小.
推荐套卷
.
如图，四棱锥P-ABCD的侧面PAD垂直于底面ABCD，∠ADC=∠BCD=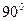,PA=PD=AD=2BC=2，CD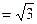,M在棱PC上，N是AD的中点，二面角M-BN-C为.
（1）求的值；
（2）求直线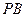与平面BMN所成角的大小.
粤公网安备 44130202000953号