如图，M、N、P分别是正方体ABCD－A1B1C1D1的棱AB、BC、DD1上的点．
(1)若＝，求证：无论点P在D1D上如何移动，总有BP⊥MN；
(2)若D1P：PD＝1∶2，且PB⊥平面B1MN，求二面角M－B1N－B的余弦值；
(3)棱DD1上是否总存在这样的点P，使得平面APC1⊥平面ACC1？证明你的结论．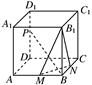
相关试题
的取值范围；
，使得函数
在区间
上为减函数，且最大值为1，若存在，求出
：实数
满足
，其中
；命题
：实数
且
的必要不充分条件，求实数
的取值范围．
中，
；
，求证数列
是等比数列；
，求证：数列
是等差数列；
：方程
表示焦点在
轴上的双曲线，
：方程
=(
一
)
为椭圆
内的一定点，过P点引一直线，与椭圆相交于
两点，且P恰好为弦AB的中点，如图所示，求弦AB所在的直线方程及弦AB的长度。
推荐套卷
如图，M、N、P分别是正方体ABCD－A1B1C1D1的棱AB、BC、DD1上的点．
(1)若＝，求证：无论点P在D1D上如何移动，总有BP⊥MN；
(2)若D1P：PD＝1∶2，且PB⊥平面B1MN，求二面角M－B1N－B的余弦值；
(3)棱DD1上是否总存在这样的点P，使得平面APC1⊥平面ACC1？证明你的结论．
粤公网安备 44130202000953号