下图为丹桂华庭内的两幢楼，它们的高AB=CD=30m，现需了解甲楼对乙楼的采光的影响情况。当太阳光与水平线的夹角为30°时。试求：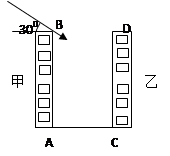
1）若两楼间的距离AC=24m时，甲楼的影子，落在乙楼上有多高？
2）若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当有多远？
列方程：（每小题4分，共8分．）
；
；
，然后在取一组m,n的值代入求值相关知识点
推荐套卷
下图为丹桂华庭内的两幢楼，它们的高AB=CD=30m，现需了解甲楼对乙楼的采光的影响情况。当太阳光与水平线的夹角为30°时。试求：
1）若两楼间的距离AC=24m时，甲楼的影子，落在乙楼上有多高？
2）若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当有多远？
粤公网安备 44130202000953号