在棱长为1的正方体ABCD—A1B1C1D1中，E，F，G分别为棱BB1，DD1和CC1的中点．
（Ⅰ）求证：C1F//平面DEG；
（Ⅱ）求三棱锥D1—A1AE的体积；
（Ⅲ）试在棱CD上求一点M，使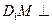
平面DEG．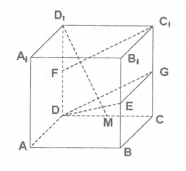
相关试题
的右焦点为
，点
在椭圆上．
在圆
上，且
在第一象限，过
,
两点，求证：△
的周长是定值．
，直线
．
，直线
与圆
恒有两个交点；
中，侧棱垂直底面，
是棱
的中点．
⊥平面
；
，设命题
函数
是
上的单调递减函数；命题
：函数
的定义域为
”是真命题，“
”是假命题，求实数
的取值范围．相关知识点
推荐套卷
在棱长为1的正方体ABCD—A1B1C1D1中，E，F，G分别为棱BB1，DD1和CC1的中点．
（Ⅰ）求证：C1F//平面DEG；
（Ⅱ）求三棱锥D1—A1AE的体积；
（Ⅲ）试在棱CD上求一点M，使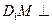平面DEG．
粤公网安备 44130202000953号