本小题満分15分)
已知 为直角梯形,
为直角梯形,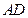 //
// ,
, ,
, 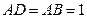 ,
,  ,
,  平面
平面 ,
,
(1)若异面直线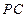 与
与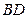 所成的角为
所成的角为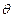 ,且
,且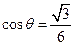 ,求
,求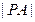 ;
;
(2)在(1)的条件下,设 为
为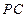 的中点,能否在
的中点,能否在 上找到一点
上找到一点 ,使
,使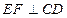 ?
?
(3)在(2)的条件下,求二面角 的大小.
的大小.
推荐套卷
本小题満分15分)
已知 为直角梯形,
为直角梯形,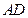 //
// ,
, ,
, 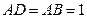 ,
,  ,
,  平面
平面 ,
,
(1)若异面直线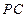 与
与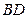 所成的角为
所成的角为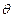 ,且
,且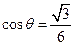 ,求
,求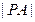 ;
;
(2)在(1)的条件下,设 为
为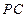 的中点,能否在
的中点,能否在 上找到一点
上找到一点 ,使
,使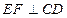 ?
?
(3)在(2)的条件下,求二面角 的大小.
的大小.