.(本小题满分16分)
已知函数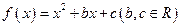 ,并设
,并设 ,
,
(1) 若
若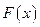 图像在
图像在 处的切线方程为
处的切线方程为 ,求
,求 、
、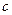 的值;
的值;
(2)若函数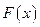 是
是 上单调递减,则
上单调递减,则
① 当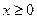 时,试判断
时,试判断 与
与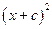 的大小关系,并证明之;
的大小关系,并证明之;
② 对满足题设条件的任意 、
、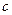 ,不等式
,不等式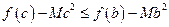 恒成立,求
恒成立,求 的取值范围
的取值范围
推荐套卷
.(本小题满分16分)
已知函数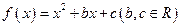 ,并设
,并设 ,
,
(1) 若
若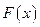 图像在
图像在 处的切线方程为
处的切线方程为 ,求
,求 、
、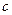 的值;
的值;
(2)若函数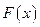 是
是 上单调递减,则
上单调递减,则
① 当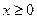 时,试判断
时,试判断 与
与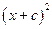 的大小关系,并证明之;
的大小关系,并证明之;
② 对满足题设条件的任意 、
、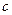 ,不等式
,不等式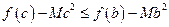 恒成立,求
恒成立,求 的取值范围
的取值范围