(本小题满分10分)选修4-4:坐标系与参数方程
如图,已知点 ,
,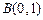 ,圆
,圆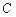 是以
是以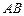 为直径的圆,直线
为直径的圆,直线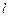 :
: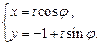
( 为参数).
为参数).
(Ⅰ)写出圆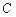 的普通方程并选取适当的参数改写为参数方程;
的普通方程并选取适当的参数改写为参数方程;
(Ⅱ)过原点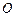 作直线
作直线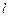 的垂线,垂足为
的垂线,垂足为 ,若动点
,若动点 满足
满足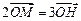 ,当
,当 变化时,求点
变化时,求点 轨迹的参数方程,并指出它是什么曲线.
轨迹的参数方程,并指出它是什么曲线.
推荐套卷
(本小题满分10分)选修4-4:坐标系与参数方程
如图,已知点 ,
,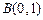 ,圆
,圆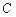 是以
是以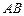 为直径的圆,直线
为直径的圆,直线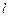 :
: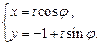
( 为参数).
为参数).
(Ⅰ)写出圆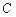 的普通方程并选取适当的参数改写为参数方程;
的普通方程并选取适当的参数改写为参数方程;
(Ⅱ)过原点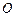 作直线
作直线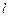 的垂线,垂足为
的垂线,垂足为 ,若动点
,若动点 满足
满足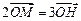 ,当
,当 变化时,求点
变化时,求点 轨迹的参数方程,并指出它是什么曲线.
轨迹的参数方程,并指出它是什么曲线.