甲乙两人各有一个箱子，甲的箱子里面放有
个红球，
个白球（
，且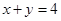
）；乙的箱子里面放有2个红球，1个白球，1个黄球．现在甲从自己的箱子里任取2个球，乙从自己的箱子里任取1个球．若取出的3个球颜色都不相同，则甲获胜．
(1)试问甲如何安排箱子里两种颜色球的个数，才能使自己获胜的概率最大？并求甲获胜的概率的最大值.
(2) 当甲获胜的概率取得最大值时，求取出的3个球中红球个数
的分布列．
相关试题
为首项为1的等差数列，其公差
，且
成等比数列.
,数列
的前
项和
,求
.
中，
分别是内角
所对的边，且
。
的大小； 
，且
，求
在R上的最大值为5.
的单调递减区间。
的最小值为3，求
的值；
的解集.
（
为参数），
（
为参数）.
的方程为普通方程，并说明它们分别表示什么曲线；
的左顶点且倾斜角为
的直线
交曲线
于
两点，求
.推荐套卷
甲乙两人各有一个箱子，甲的箱子里面放有个红球，个白球（，且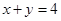）；乙的箱子里面放有2个红球，1个白球，1个黄球．现在甲从自己的箱子里任取2个球，乙从自己的箱子里任取1个球．若取出的3个球颜色都不相同，则甲获胜．
(1)试问甲如何安排箱子里两种颜色球的个数，才能使自己获胜的概率最大？并求甲获胜的概率的最大值.
(2) 当甲获胜的概率取得最大值时，求取出的3个球中红球个数的分布列．
粤公网安备 44130202000953号