由方程
所确定的
的函数关系记为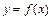
.给出如下结论：
① 
是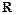
上的单调递增函数；
②对于任意
，
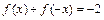恒成立；
③存在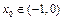
，使得过点
，
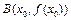的直线与曲线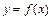恰有两个公共点．
其中正确的结论为 (写出所有正确结论的序号) ．
的首项及公差均是正整数，前
项和为
，且
，
，
，则
=.
为互不相等的正整数，方程
的两个实根为
，且
，则
的最小值为___________.
,当
的最小值时，椭圆的离心率
．
满足
则
的取值范围是．
的面对角线
上存在一点
使得
最短，则
推荐套卷
由方程所确定的的函数关系记为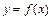.给出如下结论：
① 是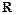上的单调递增函数；
②对于任意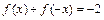，恒成立；
③存在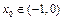，使得过点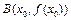，的直线与曲线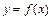恰有两个公共点．
其中正确的结论为 (写出所有正确结论的序号) ．
粤公网安备 44130202000953号