（本小题满分13分）
给定椭圆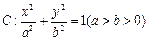
，称圆心在坐标原点
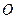，半径为
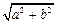的圆是椭圆
的“伴随圆”． 若椭圆C的一个焦点为
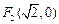，其短轴上的一个端点到
距离为
．
（Ⅰ）求椭圆及其“伴随圆”的方程；
（Ⅱ）若过点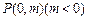
的直线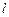
与椭圆C只有一个公共点，且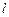截椭圆C的“伴随圆”所得的弦长为
，求
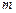的值；
（Ⅲ）过椭圆C“伴椭圆”上一动点Q作直线
，使得与椭圆C都只有一个公共点，试判断直线的斜率之积是否为定值,并说明理由.
相关试题
，向量
，函数
．
的最小正周期
；
分别为
内角
的对边，
为锐角，
，且
恰是
上的最大值，求
．
.
，且对任意实数
均有
，求
的表达式；
时，设
，求g（x）最小值.
的定义域;
；
．
在
上的最大值比最小值大2，求实数
的值．推荐套卷
（本小题满分13分）
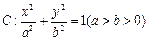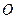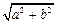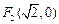给定椭圆，称圆心在坐标原点，半径为的圆是椭圆的“伴随圆”． 若椭圆C的一个焦点为，其短轴上的一个端点到距离为．
（Ⅰ）求椭圆及其“伴随圆”的方程；
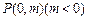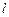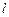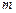（Ⅱ）若过点的直线与椭圆C只有一个公共点，且截椭圆C的“伴随圆”所得的弦长为，求的值；
（Ⅲ）过椭圆C“伴椭圆”上一动点Q作直线，使得与椭圆C都只有一个公共点，试判断直线的斜率之积是否为定值,并说明理由.
粤公网安备 44130202000953号