在某次竞赛活动中(竞赛以笔试形式进行),文科班有2名同学参加数学竞赛,另有2名同学参加英语竞赛;理科班有2名同学参加数学竞赛,另有3名同学参加英语竞赛。后由于某种原因,参加数学和英语竞赛的同学各有一名同学交换考试。
(1)求参加数学竞赛恰有2名文科同学的概率。
(2)求参加数学竞赛的文科同学数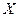 的分布列。
的分布列。
推荐套卷
在某次竞赛活动中(竞赛以笔试形式进行),文科班有2名同学参加数学竞赛,另有2名同学参加英语竞赛;理科班有2名同学参加数学竞赛,另有3名同学参加英语竞赛。后由于某种原因,参加数学和英语竞赛的同学各有一名同学交换考试。
(1)求参加数学竞赛恰有2名文科同学的概率。
(2)求参加数学竞赛的文科同学数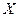 的分布列。
的分布列。