、已知函数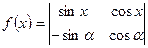 ,
,
 ,
, 是参数,
是参数,  ,
,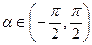 ,
,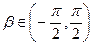
(1)、若 ,判别
,判别 的奇偶性;
的奇偶性;
若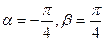 ,判别
,判别 的奇偶性;
的奇偶性;
(2)、若 ,
, 是偶函数,求
是偶函数,求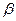

(3)、请你仿照问题(1)(2)提一个问题(3),使得所提问题或是(1)的 推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
将根据写出真命题所体现的思维层次和对问题探究的完整性,给予不同的评分。
相关知识点
推荐套卷
、已知函数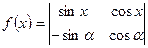 ,
,
 ,
, 是参数,
是参数,  ,
,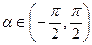 ,
,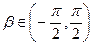
(1)、若 ,判别
,判别 的奇偶性;
的奇偶性;
若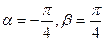 ,判别
,判别 的奇偶性;
的奇偶性;
(2)、若 ,
, 是偶函数,求
是偶函数,求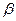

(3)、请你仿照问题(1)(2)提一个问题(3),使得所提问题或是(1)的 推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
将根据写出真命题所体现的思维层次和对问题探究的完整性,给予不同的评分。