（本小题满分12分）
已知圆C的圆心为原点O，且与直线x+y+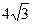
=0相切.
（1）求圆C的方程；
（2）点P在直线x=8上，过P点引圆C的两条切线PA、PB，切点为A、B,求证：直线AB恒过定点.
相关试题
在
上的最大值和最小值．
，函数
的图象下方。
，
，解不等式
； （2）如果
，
，求a的取值范围
和圆
的极坐标方程分别为
．
（
的单位为:秒,
的单位为:米/秒）的速度作变速直线运动，求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?相关知识点
推荐套卷
（本小题满分12分）
已知圆C的圆心为原点O，且与直线x+y+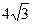=0相切.
（1）求圆C的方程；
（2）点P在直线x=8上，过P点引圆C的两条切线PA、PB，切点为A、B,求证：直线AB恒过定点.
粤公网安备 44130202000953号