本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.
相关知识点
推荐套卷
 (万元)与投入资金
(万元)与投入资金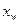 (万元)成正比例关系,且当投入资金为6万元时,可获利润1.5
(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5 万元。生产R型产品所获利润
万元。生产R型产品所获利润 (万元)与投入资金
(万元)与投入资金 (
( 万元)满足关系
万元)满足关系 ,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少? ,在
,在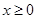 时的图象是如图所示的抛物线的一部分,
时的图象是如图所示的抛物线的一部分,
 的定义域为集合A,
的定义域为集合A,
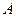 ;
; ,求
,求 的取值范围;
的取值范围; ,
,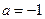 ,求
,求 及
及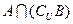
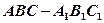 中,
中,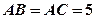 ,
,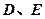 分别为
分别为 的中点,四边形
的中点,四边形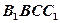 是边长为
是边长为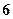 的正方形。
的正方形。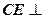 平面
平面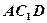 ;
;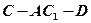 的余弦值。
的余弦值。
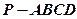 中,底面
中,底面 是矩形,且
是矩形,且 ,
,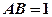 ,
, 平面
平面 分别是线段
分别是线段 的中点。
的中点。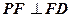 ;
; 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号