（本小题共14分）
已知函数
（1）试用含有a的式子表示b，并求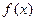
的单调区间；
（2）设函数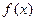的最大值为
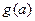，试证明不等式：
（3）首先阅读材料：对于函数图像上的任意两点
，如果在函数图象上存在点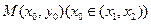
，使得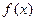在点M处的切线
，则称AB存在“相依切线”特别地，当
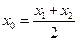时，则称AB存在“中值相依切线”。
请问在函数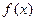的图象上是否存在两点，使得AB存在“中值相依切线”？若存在，求出一组A、B的坐标；若不存在，说明理由。
相关试题
的右焦点
作斜率
的直线交椭圆于
，
两点，且
与
共线.
为椭圆上任意一点，且
. 证明：
为定值.
.
时，求关于
的不等式
解集；
时，若
恒成立，求实数
的最大值.
}的公差
，它的前
项和为
，若
，且
成等比数列.
}的前
，求证：
．
：
的离心率为
，其中左焦点
．
与椭圆
两点，且线段
的中点
在圆
上，求
的值．
中，
，且
是
和
的等差中项．
满足
，求
项和
．推荐套卷
（本小题共14分）
已知函数
（1）试用含有a的式子表示b，并求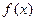的单调区间；
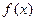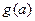（2）设函数的最大值为，试证明不等式：
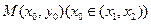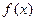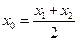（3）首先阅读材料：对于函数图像上的任意两点，如果在函数图象上存在点，使得在点M处的切线，则称AB存在“相依切线”特别地，当时，则称AB存在“中值相依切线”。
请问在函数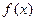的图象上是否存在两点，使得AB存在“中值相依切线”？若存在，求出一组A、B的坐标；若不存在，说明理由。
粤公网安备 44130202000953号